私の時代は、小学生に「一番大きな数は？」と聞くと「百億万円」だった（古い！）のですが、最近は、「無量大数」と答える・・・という記事を読んだことがあります。
「無量大数」は 1000000000000000000000000000000000000000000000000000000000000000000000 と、1のあとに0が68個も付く数字ですが、きっと小学生には理解できないでしょうし、きっと、大人でもわからない大きな数でしょう。
この記事は、役立つこともなさそうな雑学知識ですが、興味あれば読んでみてください。
「位取り」は、日本人に酷すぎ
コンピュータのメモリ容量などでは、K・M・G・T・P・E・Z・Y という表示があります。
キロ・メガ・ギガ・・・の頭の文字ですが、これは国際単位系（SI単位系）の接頭辞（接頭語）で、kilo mega giga tera peta exa zetta yotta を表しています。
アメリカなどの諸外国は、ｋ＝1,000 M=1,000,000 G＝1,000,000,000 のように、「3桁区切り」になっていますが、日本は、万＝1 0000 億＝1 0000 0000 兆＝1 0000 0000 0000 のように、「4桁区切り」で、この違いで苦労させられたことはありませんか？
今では、「読み方は日本式、書き方は西洋式」というようになっているのですが、これの由来は・・・
この「3桁区切り」が導入されてのは、明治6年。 西洋簿記学「帳合の法」を訳した福沢諭吉が、それまでの漢数字ではなく、「アラビア数字の横書き数字では、3桁区切りが便利だ」としたことが元になっています。
そして、昭和27年（1962年）に、「公用文作成の要領」で、「3桁ごとにコンマで区切る・・・」という、内閣官房長官の通達があって以降、「3桁区切り」が標準になった・・・ということのようです。（NHKの「チコちゃんに叱られる」で、これが取り上げられていました）
大きな数といえば、まず、「コンピューターの記憶容量」が頭に浮かびます。
コンピュータは外国から来たものなので、1ギガ、1テラなどは、そのままでイメージして、日本の4桁区切りの数字に直して考えることはしないと思いますが、1ギガ＝1000,000,000＝10億 1テラ＝1,000,000,000,000＝1兆 というように換算すると大変です。
コンピュータ用語では、位取りのややこしさに加えて、1メガバイトは100万バイトではなく、1,024,000バイト（24キロバイトも違っている数値）なのですが、これはあとで紹介しています。
いずれにしても、このように、改めてゼロをつけて書いてみると、非常に大きな数ということがわかります。
PR
大きな数は「10の何乗」で表すと、少しだけわかりやすい・・・？
物理の世界では、一般的には、大きな数字は、「10の何乗」という言い方をします。
1キロメーター（km）は10の3乗メーター、つまり1,000ｍ （1のあとに0が3こ）で、メガは 10の6乗で、この「6乗」は「1のあとに、0が6こ」の1,000,000 という数です。
しかし、これを日本の数字で言おうとすると少し混乱が生じ始めます。
日本の数字表記では1キロ＝1000，1メガ＝100万（1,000,000）と、ここまでは、慣れもあって頭が混乱することはないのですが、次からが大変で、1ギガ＝10億 で、1テラ＝1兆、1ペタ＝1000兆、1エクサ＝100京となって、4桁ずつ進んでいる日本の桁上りとは違ってきて、だんだん分からなくなってきます。
下に色分けしたように、日本の桁数と欧米の接頭辞は食い違っています。
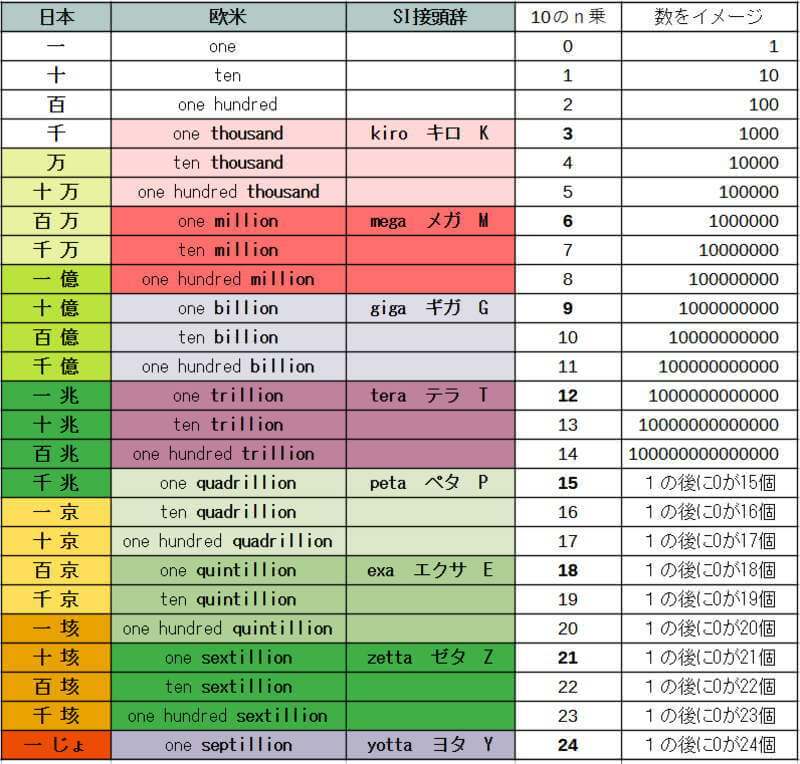
この、最後に書いた「じょ」は、のぎへん（禾）に予と書くのですが、これは、普通では文字変換できない「国字（和製漢字）」で、それらの国字も、JISでは決められているので、コード入力をして「𥝱」とすると表示させることは出来るのですが、使うブラウザによっては、うまく表示されないという、「ほとんど使わない文字」です。（それもあって、ここでは、ひらがなにしました）
英語表記では１kiro＝1thousand（サウザンド）、1mega＝1million（ミリオン）、1giga＝1trillion（トリリオン）というように、3ケタづつの呼び方は呼応していますから、英語圏では分かりやすいのですが、日本の数字は4桁区切りなのでずれてくるので、日本読みに対比させようとすると、覚えにくくなってしまいますね。
PR
このように、欧米は「0が3つ」ごとに単位が変わる「文化」なので、桁区切りでは、日本の文化の4ケタほど苦労はないのでしょう。
私の場合を振り返ると、小学校では最初に、「桁区切りは4桁区切り」で習い、6年になって「通常は3桁区切りで、会計では、3桁区切りで表記されます・・・」と教えられて、頭の切り替えができずに困ったことを覚えています。
4桁区切りがわかりやすいけれども、今、それを使うとさらに混乱しそう
1,0000,0000（＝100,000,000） は「一億」という数です。
現在は4桁区切りで書く書き方はしないことになっています。 だから、4桁区切りで書くと、余計に混乱します。
しかし、下の「5つ玉（五つ珠）」のそろばんを使っている時代には、4桁区切りが普通だったのです。
以前のそろばん（5つ玉・4桁区切り）
今のそろばん（4つ玉・3桁区切り）
「5つ玉のそろばん」や4桁区切り、さらには、上の玉（珠）が2つあるものなどを使うことができる人はほとんどいなくなっているでしょう。
上の5つ玉は、明治生まれの父は5つ玉を使っていて、家にあったのを覚えています。
昭和の戦争のあとに、日本の文化が完全に変わってしまったようなのですが、日本人は、いとも簡単に外国文化を吸収してしまう民族なので、変化に対する抵抗も少なかったようですが、4桁文化の本家本元の「中国（China)」の人は、日本人以上に苦労しているのではないかと思います。
しかし、3桁区切りは「国際化」の一環ですので、どうすることも出来ませんし、昭和生まれの私とちがって、最近の若い方は、3桁区切りに違和感や抵抗はないのでしょうね。
PR
でも、英国でも、米国でも、日本のように、問題点はあるようです
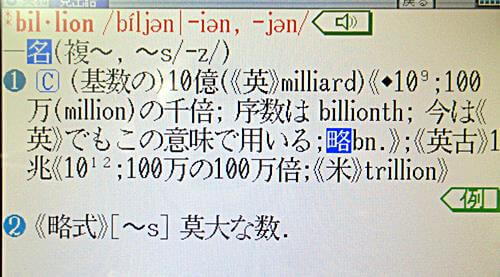
話は脱線しますが、「billion」を電子辞書で調べたところ、上のような記事が書いてあります。
billion は10億ですが、イギリス（英国）ではそれを milliard と言うようで、昔のイギリスでは、billion は10億ではなく1兆を表していて、それが次第にアメリカ式の10億に移っている・・・と書かれています。 つまり、イギリスでも、大変なことがある（または「あった」）ようですね。
アメリカはどうかといえば、やはり今でも「ヤード・ポンド」が残っていますので、これもやはり混乱しているでしょうし、日本でも、未だに古い単位の「坪・升・合」などが残っているのですから、どこの国でも、共通化（国際化）の過程では、何も問題がない・・・ということではなさそうです。
大数（大きな数）は決められているけれども使うことはなさそう
この上のK・M・G・・・は、キロ、メガ、ギガ・・・で、下段の 恒河沙～無量大数 は、「塵劫記」という書物に書かれた、一十百千万に続く、非常に大きな数の一部です。
恒河沙（こうがしゃ・ごうがしゃ）阿僧祇（あそうぎ） ・・・は、一十百千万億兆……のあとに続く大きな数で、これらは実際に用いられることはなさそうな大きな数字ですが、「数（の単位）がある」ということに驚きます。
欧米でも、K・M・G・・・に続く、もっと上の数字の言い方があります。
「塵劫記」に書かれた、最も大きな数とされている「無量大数」についても、https://id.fnshr.info/2017/08/27/large-numbers/ さんのHPを見ると、「英語では、無量大数は one hundred unvigintillion という」と書いてあって、その記事では、英語では、「無量大数ｘ無量大数＝＊＊＊」という数も表現できるようです。
もちろん、これらは、「言葉の遊び」と言ってもよく、実際の数字として使うことはないでしょう。
すごい大きな数を実感したいなら、自分で書いてみるといい
ここで、下に、SI接頭辞のかなり大きい数の yotta（ヨタ）と「無量大数」のゼロの数を書いてみました。
1yotta ＝10000000000000000000000000
無量大数 ＝1000000000000000000000000000000000000000000000000000000000000000000000
「yotta」は1の後ろに0が24個もつく大きな数ですが、無量大数は1の後ろに0が68もつく数です。 すごいと言うよりも、「無駄」な感じもします。
すごい増えたコンピュータの記憶容量
近年、記憶容量（バイト数）などで目にするようになった「テラバイト」ですが、これは、1,000,000,000,000バイト と、1の後ろにゼロが12個付きます。
「私が初めて買ったパソコンのNECのPC8001のメモリーは、標準が16kバイトで、それを32ｋに増設して20万円で購入した・・・」ということを私の息子に話すと、息子は「キロ？」という感じで呆れているのですが、その、1979年から30年も経たないうちに、PCの記憶容量は、10の3乗の「キロ」から10の12乗の「テラ」になりました。そして、その記憶容量にも関わらず、PCの価格は当時の32Kバイトパソコンの半額以下で購入できるというのにも首を傾げます。
記憶容量のバイト数は、少し前にはギガであったものが、テラやペタという単位も耳にするようになってきました。しかし、そう言われても、結局のところ、「すごい数」と言うだけで、何がすごいのかも、頭が麻痺して、比較もままなりません。
PR
つぎに、PCなどで使われる、テラバイトなどに関係する2進数について少しだけ取り上げます。
2進数はコンピュータで一躍身近なものになりました
ここまでは10進数での話でしたが、コンピュータの世界では2進数が基本です。
そのために、 0，1，10，11，100・・・と増えていく世界では、2の10乗（1024）が1キロバイトとなっているのですが「なぜ？」と言われても、こう決められているのです。
つまり、K（キロ）は1000ではないのですが、世の中はこれで動いていますので、不可解だと悩んでも仕方がありません。
つまり、「キロ」というのは、10進数では1000倍の接頭語ですが、2進数では習慣的に、2の10乗の1024が1キロバイトとして扱われるのです。
そうすると、1メガバイトが 1,024,000バイト、1ギガバイトが 1,024,000,000バイト、1テラバイトが 1,024,000,000,000バイト・・・ですが、混乱を避けるために、一応は、2進数を表す「バイナリー」という用語を後ろにつけて、「キロバイナリーバイト（略してKiBまたはKibi：キビバイト）と呼ぶように定められています。
しかし、この言い方はそんなに普及していなくて、一般的には、商品では、「メガバイト」「テラバイト」と表示されていて、その詳細については、断り書きはないのが普通ですから、現実は、メガバイトが1,024,000バイトなのか1,000,000バイトなのかも、はっきりしない場合も多いので、気にするものでもないということですね。
つまり、どちらが正しいのかというよりも、ほとんどの人は、イメージで『大きな数』を感じているので、気にすることもないということかもしれません。
さらに加えて、ややこしいのですが、「1バイト=8ビットです」が加わると、ますます混乱します。
これらの内容も、適当なイメージで話していても、全く問題なく話ができますので、一般人レベルでは、それはそれでいいのかもしれません。
情報の世界で用いられる、さらに大きな数
2進数の情報関連の世界では、10進数の接頭語のyotta（10の24乗）以上の数字についても、すでに決められています。覚える必要はないのでしょうが、雑学知識として見ておいてください。
Kibi bite（記号はKiB）が210（1024バイト）ですが、それ以上の数で、
Mebi Byte（記号Mi =2の20乗）
Gibi Byte（記号Gi =2の30乗）
Tebi Byte（記号Ti =2の40乗）
Pebi Byte（記号Pi =2の50乗）
Exbi Byte（記号Ei =2の60乗）
Zebi Byte（記号Zi =2の70乗）
Yobi Byte（記号Yi =2の80乗）
などの呼び方があります。当面は使うことが無いでしょうが、すでに決められています。これは、 K・M・G・T・P・E・Z・Y というSI単位系の接頭辞と同じ順になっているので、違和感は少ないでしょう。
ともかく、ここで、最も大きいYobi Byteは、2の80乗は 1,208,925,819,629,174,706,176バイトという、とてつもなく大きい数字です。
これはこれですごい数なのですが、「無量大数の10の68乗」から考えると、そんなに大きいと感じないのも、変な感じです。
あなたは大きな数字といえば・・・宇宙ですか？
ちなみに、とてつもない「大きな数字」のイメージの筆頭では、宇宙の大きさや「光年」という単位が頭に浮かびますね。
光が1年間に進む距離が「1光年」で、秒速30万kmｘ60ｘ60ｘ24ｘ365 ですので、時速は、約9,460,800,000,000ｋｍ という距離です。
この数字でも、およそ 10の13乗km ≒ 10テラkm ≒ 10trillion という大きさのレベルです。
さらに、もっと大きい数字といえば、測定できる宇宙の果てまでの距離が「138億光年」と言う数字があり、さらに、半径450億光年が「観測できる宇宙」・・・とされていて、宇宙の直径はおよそ1000億光年・・・などの数字を見ることがあるのですが、これらの数字が、やはり、眼にする数字としては最大級といえます。
千億は1011 ですから、距離にすれば、1千億光年は、10の24乗km（10の30乗mm）という数字になって、これが現実に考えられそうな「大きな数」かもしれませんが、宇宙物理学などでは、このような数字は使われずに、「パーセク」という数字が使われます。
パーセクは、年周視差1秒角という、非常に小さな角度に相当する距離で、約3.3光年、31兆キロ弱ですが、そうなると、宇宙の大きさや、その果てにある星までの距離がイメージできるかといえば、素人には無理で、宇宙の端までの距離がわかっても、ほとんど実用的ではありませんので、このような表現や数字は、まず、一般の人が、たとえ知っていても、使うこともないものなのでしょうね。
次は、「小さな数」についても見てみましょう
日本では、1以下の数は、野球の打率などの「分・厘・毛……」が現在でも聞かれますが、それ以下はほとんど見かけることもありません。
分は0.1、厘は0.01、毛は0.001の単位ですが（0.1は10のマイナス1乗、0.01は10のマイナス2乗といいます）、分厘毛の呼び方自体もあまり使われなくなっていますから、使われる小さい数については、SI接頭辞による表示や言い方で問題なさそうです。
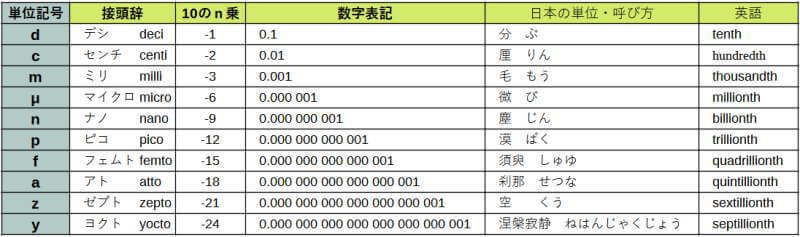
1627年に数学者の「吉田光由」という人が、中国の「算法統宗」というものを参考にして、それをまとめた中の「単位の分類（命数法）」に書かれているのが一般的になっているようですが、この本でも、新しい改定版が出版されるごとに、書いてある内容が変わっていたらしいので、この表も参考程度に見ておいてください。
蛇足ですが、「オングストローム」という単位をよく耳にします。
これは、SI単位ではない「長さ」の単位で、SI単位で言うと、0.1nm（ナノメーター）という単位です。
これは、光の波長や原子の大きさなどを言う場合に用いられますが、音の響きがいいし、かっこいい感じに聞こえるので、SI単位ではないのですが、よく使われています。
現在は、SI単位系で言うのが標準になってきていますので、このオングストロームも、かつては、高気圧・低気圧で使われた「ミリバール」と同様に、今後は見聞きすることが少なくなっていくでしょう。
PR
実用的な小さな数字といえば…
通常の機械的な測定器や光学顕微鏡では、1マイクロメータ（ミクロン：1/1000mm：記号μm）程度が確認できる最小長さです。
いっとき話題になった「コロナウイルス」は100nm（0.1マイクロメータ）といわれており、1マイクロメータ以下は、電子顕微鏡でないと見えない大きさです。ウイルスは非常に小さいのです。
最近聞くことが多くなった「ナノ」ですが、10のマイナス9乗と、気の遠くなるような小さい数字です。
しかしさらに、コンデンサの容量では、さらに小さい「ピコ」という単位が生きています。「ピコファラッド＝pF」という容量のコンデンサは、電子機器にはたくさん使われています。
さらに、レーザー加工機の波長や時間では、「フェムト秒」という言葉を聞くことがあります。
フェムト（f）は10のマイナス15乗で、これらのレーザー波長は、実際に使われて稼働しています。
これらは実際に使われている小さい数です。
究極の小さい数
そして、究極の小さい単位では、現代物理学ででてくる単位で「プランク単位」というものがあります。
これを用いると、いろいろな物理法則や方程式を簡単に表すことができる・・・というのですが、そこで用いる「プランク長」は、現在のSI単位系では、1.62ｘ10のマイナス35乗メートルという、非常に小さな数字です。
さらに、量子物理学の世界では、「プランク時間」というものがあり、光子がプランク長を通過する時間＝5.4ｘ10のマイナス44乗秒 という単位があります。
どうもそれが、現在で考えられる、最小の長さ単位の数字と言えるかもしれません。
これによれば、光がプランク時間で進む距離で長さで上の宇宙の直径を表すと、「10の61乗プランク長さ」というすごい数字になります。
そうなると、この数字のゼロの数は、「ゼロが68個の無量大数」に、もう少しで届きそうな数字です。
もちろん、現在の物理学では、プランク長以下のものが存在する・・・という考え（もちろん仮説ですが）もあるようです。しかし、プランク長も宇宙の大きさも、普通人には認識できない範囲の数ですので、実用や知識には関係なさそうなものですが、物理学の世界では、そんなところにまで考え方が及んでいることに驚きます。
以上になります。 最後はだらだらとした内容になってしまいましたが、数の話はいかがだったでしょうか？ 私も、これを書きながら、自分の頭を整理してきたのですが、この雑学知識が、どこかで、何かのお役に立てば幸いです。
（来歴）R1.10記事作成 R4.5に見直し・サイト変更 R5.11月に文章中の指数表記変更 R6.4見直し
コメント